Discrete Dislocation Plasticity

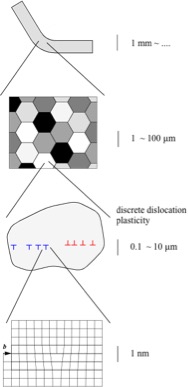
Metal plasticity is a multiscale phenomenon. It starts at the smallest scale in the form of line defects in the atomic lattice —dislocations—, which mediate slip on crystallographic planes, whose collective effect on the macroscopic scale emerges as plastic deformation. Each size scale has its own description, tailored to the emergent phenomena at that scale, and its own range of applicability.

Our work focuses on plasticity at size scales of tens of micrometers and below, by means of discrete dislocation dynamics.

This approach:

• incorporates long-range interactions between dislocations;
• allows for solving boundary-value problems;

predicts size dependent plasticity where “smaller is harder” in a natural way once appropriate constitutive rules are formulated.

1. Plasticity in thin films

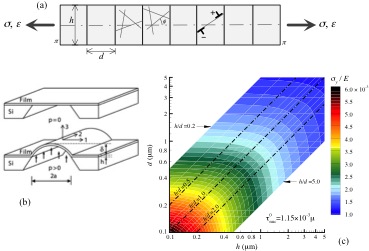
The “smaller is harder” size effect for deformation processes involving strain gradients, such as in bending or indentation, are explained in terms of Geometrically Necessary Dislocations. More surprisingly, experiments have also shown size dependent behavior in metallic thin films on a substrate. After work by our group and others had revealed that this can be explained by the piling-up of dislocations against the film-substrate interface, the next surprising finding was the size effect seen in free-standing thin films, that is, without a substrate. Bulge testing experiments (panel b in figure below) on films with a well-controlled thickness h and grain size d by Vlassak (Harvard University) provided an accurate set of data under 2D plane strain tension. After fitting two parameters in our 2D discrete dislocation model (panel a) to one particular film thickness and grain size, computations for other films yielded quantitative agreement for the entire stress-strain curves. Moreover, analysis of our simulation data provided physical understanding for this size effect and a predictive map (panel c).

PhD students: L. Nicola (now full professor at University of Padova, Italy), S.S. Shishvan (now assistant professor at University of Tabriz, Iran)

Publications (selected)

• S.S. Shishvan, L. Nicola and E. Van der Giessen (2010). Bauschinger effect in unpassivated freestanding thin films. J. Appl. Phys. 107, 093529. DOI: 10.10631/1.3407505.
• S.S. Shishvan and E. Van der Giessen (2010). Distribution of dislocation source length and the size dependent yield strength in freestanding thin films. J. Mech. Phys. Solids. 58, 678-695. DOI: 10.1016/j.jmps.2010.02.011.
• L. Nicola, Y. Xiang, J.J. Vlassak, E. Van der Giessen and A. Needleman (2006). Plastic deformation of freestanding thin films: experiments and modeling. J. Mech. Phys. Solids 54, 2089-2110.

2 . Micro- and nano-plasticity in micro and nano pillars

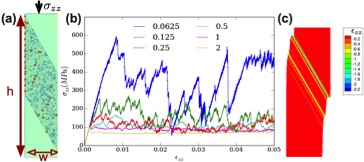
Compression of cylindrical pillars of single crystals leads to a nominally uniform stress state. The scientific community, therefore, was in awe by the 2004 Science paper of a team of US researchers who showed dramatic size effects in pillars with diameters in the range of 1 to 10 micrometers. The fascination only grew as smaller pillars, with diameters down to tens of nanometers, exhibited even stronger size effects. Moreover, a significant size dependence of the deformation modes was observed. Together with prof. Papanikolaou (now at Johns Hopkins University, Baltimore), we have developed a minimal discrete dislocation model that captures these size effects, as well as the enhanced stochastic nature of plasticity at smaller sizes.

PhD student: H. Song (now post-doc at Johns Hopkins University, Baltimore)

Publications

• S. Papanikolaou, H. Song and E. Van der Giessen (2017). Obstacles and sources in dislocation dynamics: Strengthening and statistics of abrupt plastic events in nanopillar compression. J. Mech. Phys. Solids 102, 17-29.

3 . Plastic deformation of asperities in contact and friction

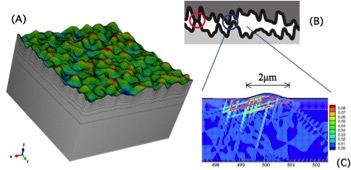
Seemingly flat surfaces are actually covered with asperities of sizes that vary from tens or hundreds of micrometers down to the atomic scale. When two of such surfaces (panel A) are pressed together, summits will interact and deform plastically even at very low applied forces. The shearing of such flattened asperities or of interlocking asperities (see panel B) during tangential load are important ingredients for the emerging friction force between the two surfaces. In view of “smaller is harder”, we have investigated the effect of size dependent plasticity on contact and friction (panel C). One of the salient conclusions of this work so far is that the linear relation between mean contact force and contact area —i.e., the cornerstone of the classical Coulomb friction law— persists, albeit that the ratio of the two increases when size dependent plasticity is taken into account.

PhD student: H. Song (now post-doc at Johns Hopkins University, Baltimore)

Publications

• H. Song, E. Van der Giessen, A.I. Vakis (2016). Erratum: "Asperity Interaction and Substrate Deformation in Statistical Summation Models of Contact Between Rough Surfaces" [Journal of Applied Mechanics, 81(4), p. 041012], J. Appl. Mech. 83 (8), 087001.
• H. Song, E. Van der Giessen, X. Liu (2016). Strain gradient plasticity analysis of elasto-plastic contact between rough surfaces. J. Mech. Phys. Solids 96, 18-28.
• H. Song, V.S. Deshpande, E. Van der Giessen (2016). Discrete dislocation plasticity analysis of loading rate-dependent static friction. Proc. Roy. Soc. London A, 472, 20150877.
• H. Song, R. J. Dikken, L. Nicola, E. Van der Giessen (2015). Plastic Ploughing of a Sinusoidal Asperity on a Rough Surface. J. Appl. Mech. 82 (7), 071006.

4 . Microplasticity and debonding in steels

Multiphase ferrous metals is a very important class of high-tech steels. Owing to a complex microstructure with different phases, these materials possess excellent fracture properties, yet can still be shaped by plastic forming. At the same time, however, plasticity causes a risk for the development of damage (the black spots in the micrograph) inside the material.

Our discrete dislocation work contributes to a national research program on the multiscale physics of failure in complex microstructures by playing the intermediate role between atomistics and macroscopic failure.

PhD student: T. Katiyar